题目描述

1. 两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

  • 2 <= nums.length <= 104
  • -109 <= nums[i] <= 109
  • -109 <= target <= 109
  • 只会存在一个有效答案

进阶：你可以想出一个时间复杂度小于 $O(n_2)$ 的算法吗？

暴力解法

许久没有写算法题的情况下，昨天打算从这个题开始练手。看完题目上来就直接开始考虑时间复杂度为$O(n)$的哈希表算法，忽略了时间复杂度为$O(n^2)$的暴力枚举算法。我觉得这是不正确的，面对一个题目，应该首先从最暴力的解决方案开始考虑，在暴力方法能实现的情况下再考虑优化时间复杂度，不然可能面临暴力方法没有实现，优化方法写不对的窘境。

所以本题目应该优先考虑暴力枚举：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int>ans;
        for(int i=0;i<nums.size();i++){
            for(int j=i+1;j<nums.size();j++){
                if(nums[i]+nums[j]==target){
                    ans.push_back(i);
                    ans.push_back(j);
                    return ans;
                }
            }
        }
        return ans;
    }
};

利用哈希表优化时间复杂度

使用std::unordered_map容器可以容易地实现一个哈希算法。不过，在实现本算法时仍然出现了问题。首先看下面的算法1，这是我第一次尝试时完成的方式：

算法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int>hashMap;
        vector<int>ans;
        for(int i=0;i<nums.size();i++){
            hashMap[nums[i]]=i;
            if(hashMap.find(target-nums[i])!=hashMap.end()){
                return {i,hashMap[target-nums[i]]};
            }
        }
        return {};
    }
};

在这种方式下出现了错误：

而经过简单的修改，下面是能通过的算法2。

算法2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int>hashMap;
        vector<int>ans;
        for(int i=0;i<nums.size();i++){
            if(hashMap.find(target-nums[i])!=hashMap.end()){
                return {i,hashMap[target-nums[i]]};
            }
            hashMap[nums[i]]=i;
        }
        return {};
    }
};

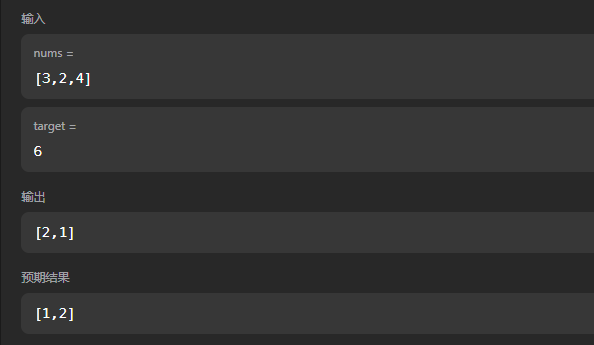
这是因为什么呢？

考虑一种特殊情况：target=2k，且nums中存在k时：

  • 如果采用算法1，当nums[i]=k时，会将{i,i}直接返回。
  • 如果采用算法2，当nums[i]=k时，由于hashMap中尚且没有nums[i]=k的情况，所以不会返回。假如在后续的遍历中存在j使得nums[i]=nums[j]=k,则将{i,j}返回，这符合我们的的预期。

正是这种特殊情况的存在，导致了算法1错误而算法2正确这样的区别。

知识点补充

vector的返回方式

注意，题目的返回类型是vector，而这不需要声明一个vector容器来返回，而是可以直接返回一个数组{a,b,c}

unordered_map常见用法

在解决很多需要使用哈希算法优化时间复杂度的题目时。unordered_map往往是一个优秀的选择。但是此前每次经过一个刷题阶段以后，我都会很快忘记这些。因此我打算将常见的用法记录在这里，避免再次忘记。

定义

1
std::unordered_map<std::string, int> map1; // 键的类型为 std::string，值的类型为 int

初始化

1
std::unordered_map<std::string, int> map = {{"Alice", 20}, {"Bob", 25}, {"Charlie", 30}};

find判空

find 方法会返回一个迭代器，如果找到了键，迭代器会指向对应的键-值对；如果没有找到键，迭代器会等于 end 方法返回的迭代器。

1
2
3
4
5
if (map.find("Alice") != map.end()) {
    std::cout << "Alice exists in the map.\n";
} else {
    std::cout << "Alice does not exist in the map.\n";
}

插入

可以使用 insert 方法来插入键-值对：

1
2
3
map.insert({"Alice", 20});
map.insert({"Bob", 25});
map.insert({"Charlie", 30});

也可以使用 operator[] 来插入或修改键-值对：

1
2
3
4
std::unordered_map<std::string, int> map;
map["Alice"] = 20;
map["Bob"] = 25;
map["Charlie"] = 30;

删除

1
map.erase(key);

遍历

1
2
3
for (auto it = map.begin(); it != map.end(); ++it) {
    std::cout << "Key: " << it->first << ", Value: " << it->second << "\n";
}